EMAの定義、知ってる？

EMAの名称に関する問題

「EMA(指数平滑移動平均線)が、なぜ『指数平滑』なのか、EMAの定義から説明しなさい。」

そもそも、EMAの定義を知らないのに、理由なんか説明できない！と読者のみなさんは思っているでしょう。

海外のトレーダーはEMAを使うことが多いですが、日本人はよく分からないからSMAを使うという人が多いのではないでしょうか。

本やネットでは、「直近の価格を重視した移動平均線」という解説で、計算式は書かれておらず、とても不親切です。

しかし、EMAを理解しないことには、それを応用して作られたMACDも理解することは出来ません。

SMAの欠点を知り、EMAを理解し、MACDも正しく使えるようになりましょう。

なので、ぜひとも今回の内容は最後まで読んで理解して欲しいです。

問題の答えを簡潔に述べるとしたら、

解答
「価格の重みが指数関数的に減っていき、SMAよりも滑らかに動くから」

前回の記事ではSMAの欠点について書きました。

移動平均線の欠点

今回はEMAが、どのようにその欠点を補うのかを説明します。

解説

EMAの定義は、

本日のEMA＝昨日のEMA+(本日の価格−昨日のEMA)×2÷(N+1)

この式を変形すると、こうなります。

本日のEMA={昨日のEMA×(N-1)+本日の価格×2}÷(N+1)

最初のEMAは、SMAで代用します。

これだと分かりづらいので、9日EMAで具体的に考えてみます。

本日のEMA＝{昨日のEMA×(9-1)+本日の価格×2)÷(9+1)
=昨日のEMA×0.8+本日の価格×0.2

本日の価格の重みは20%となります。

明日になると、どう変化するのか？

明日のEMA=本日のEMA×0.8+明日の価格×0.2

本日のEMAの中に、本日の価格の20%があるので、明日になると20%×0.8=16%

つまり、明日における本日の価格の重みは16%です。

9日SMAの価格の重みは全て等しく約11.1%なのに対し、

9日EMAは価格の重みが0.8、つまり8割づつ減っていくのです。

これが、EMAがExponential(指数)である理由です。

一般にNで表すと、

N日SMAの価格の重みは、N分の1で全て同じ。

N日EMAは価格の重みが(N-1)÷(N+1)づつ減少していく。

前回の記事で説明したSMAの欠点として、次の2つがあります。

・過去N日間の価格を全て同じ割合で扱っていること
・過去N日間以前の価格の影響が反映されないこと

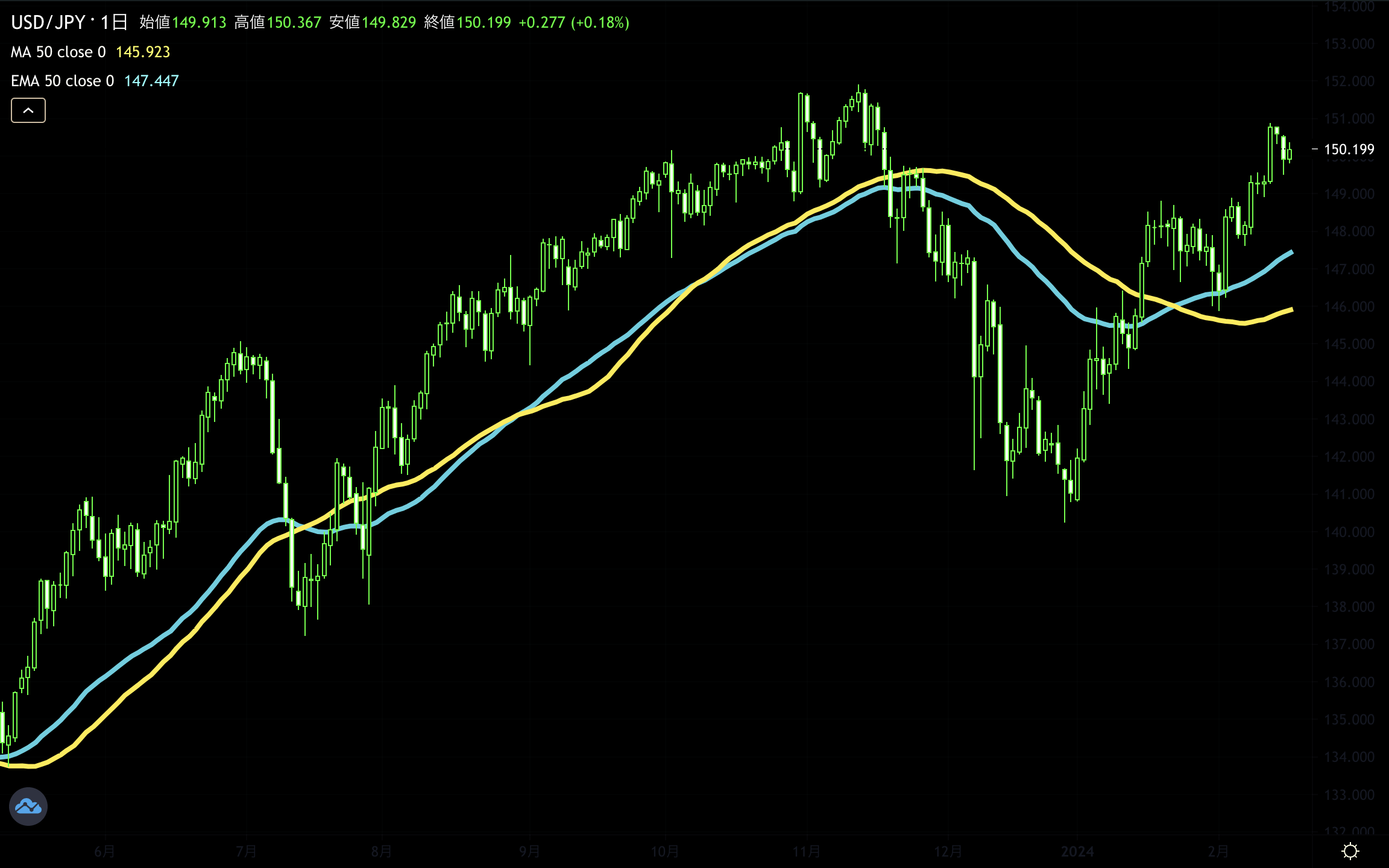
また、EMAはSMAよりも価格の変化に早く反応するため、滑らかな動きをします。

黄色い線が50SMA
水色の線が50EMA

価格により近づいて動いているのが分かります。

EMAがなぜ「指数平滑」なのかを一般にNできちんと説明すると、

解答

「定義より、N日EMAは価格の重みが(N-1)÷(N+1)づつ減少していく、つまり指数関数的に減っていき、SMAよりも価格の変化に早く反応し、滑らかな動きをするから」

また、前回の記事の問題で価格が上昇したのに移動平均線は下落したという、トレンドがどちらにあるか混乱するケースをEMAは克服しています。

EMAの定義

本日のEMA＝昨日のEMA+(本日の価格−昨日のEMA)×2÷(N+1)

この式の「本日の価格−昨日のEMA」に注目すると、次のことがわかります。

昨日のEMAよりも本日の価格が高ければ、EMAは必ず上昇する。
昨日のEMAよりも本日の価格が安ければ、EMAは必ず下落する。

なぜ、ゴールデンクロスは買いサインなのか？