【ボリンジャーバンド①】標準偏差について

標準偏差に関する問題

「ボリンジャーバンドにおいて、統計的に-2σ~＋2σの間に価格が存在する確率が95.5%という説明がある。だが、これは間違い。なぜか簡潔に説明せよ」

ボリンジャーバンドを開発したジョン・ボリンジャーさんが著書の中で、「バンド上限(+2σの位置)を超えても、それが売りシグナルではないし、バンド下限(-2σの位置)を割り込んでも、それが買いシグナルというわけではない」と、はっきり言っている。

にも関わらず、間違った売買シグナルが日本では広がっています。指標を作った本人が否定しているのに。

やはり、テクニカル指標の定義や計算式をきちんと理解しないまま使っていることが原因でしょう。

解答

「価格の動きは正規分布ではないから」

解説

ボリンジャーバンドを解説する前に標準偏差について説明します。

標準偏差を理解しないことには、ボリンジャーバンドを正しく理解できません。

標準偏差とは、データのばらつき度合いを表す数値のこと。

例えば、テストの点数で考えてみます。

5人の点数の結果が、

1組[75点、63点、57点、54点、51点]

2組[75点、74点、73点、46点、32点]

だとすると、

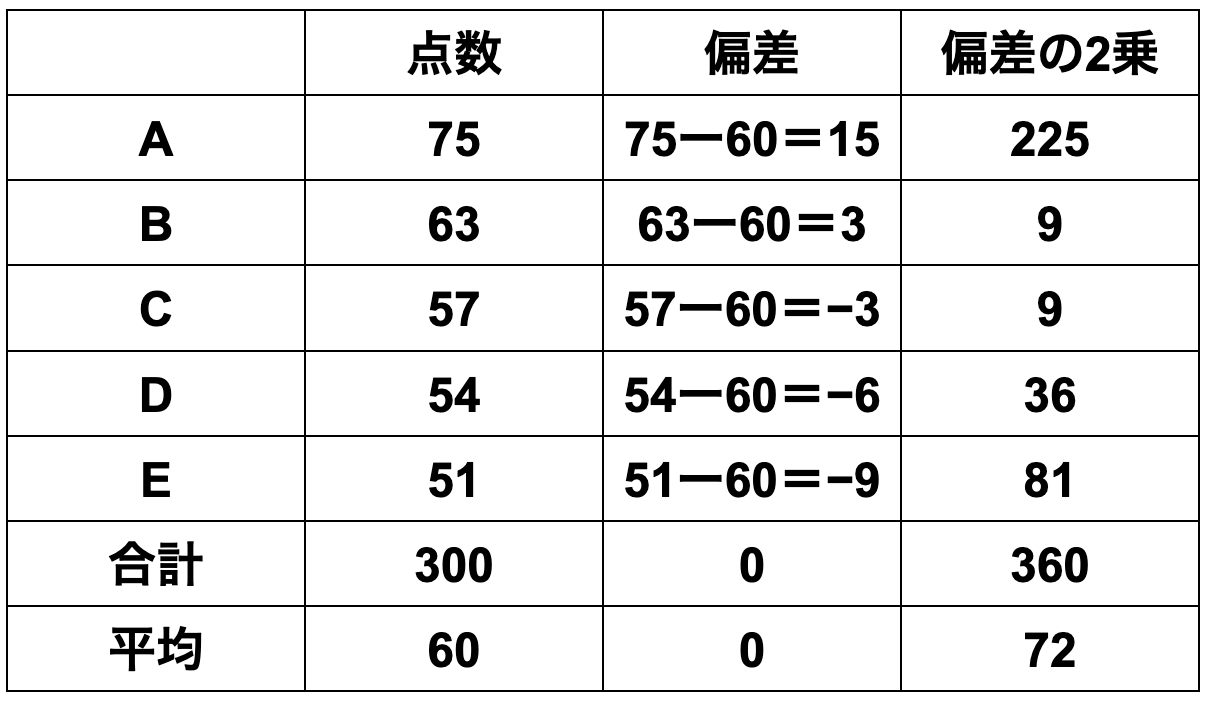
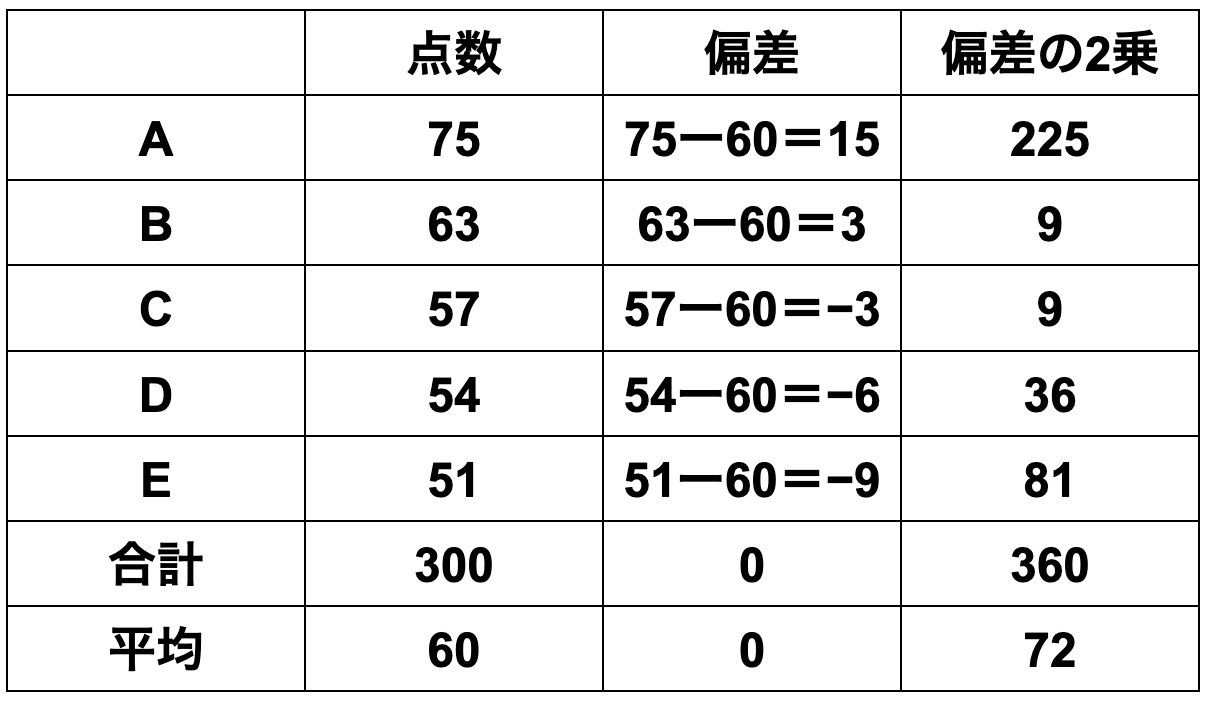
1組は、

①平均値＝各データの合計÷データ数

　　　　=(75+63+57+54+51)÷5

　　　　=60

②偏差＝各データの値−平均値

　　　＝[15、3、-3、-6、-9]

③分散＝各データの偏差の2乗の合計÷データ数

　　　＝(225+9+9+36+81)÷5

　　　＝72

④標準偏差＝√72=8.48

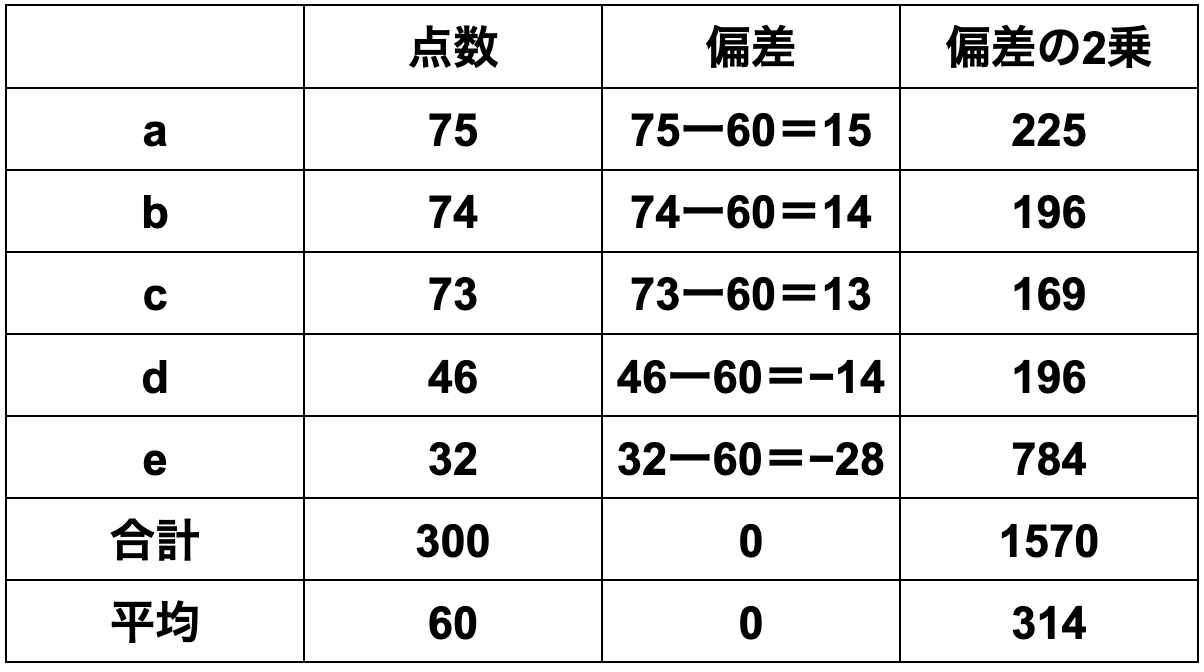
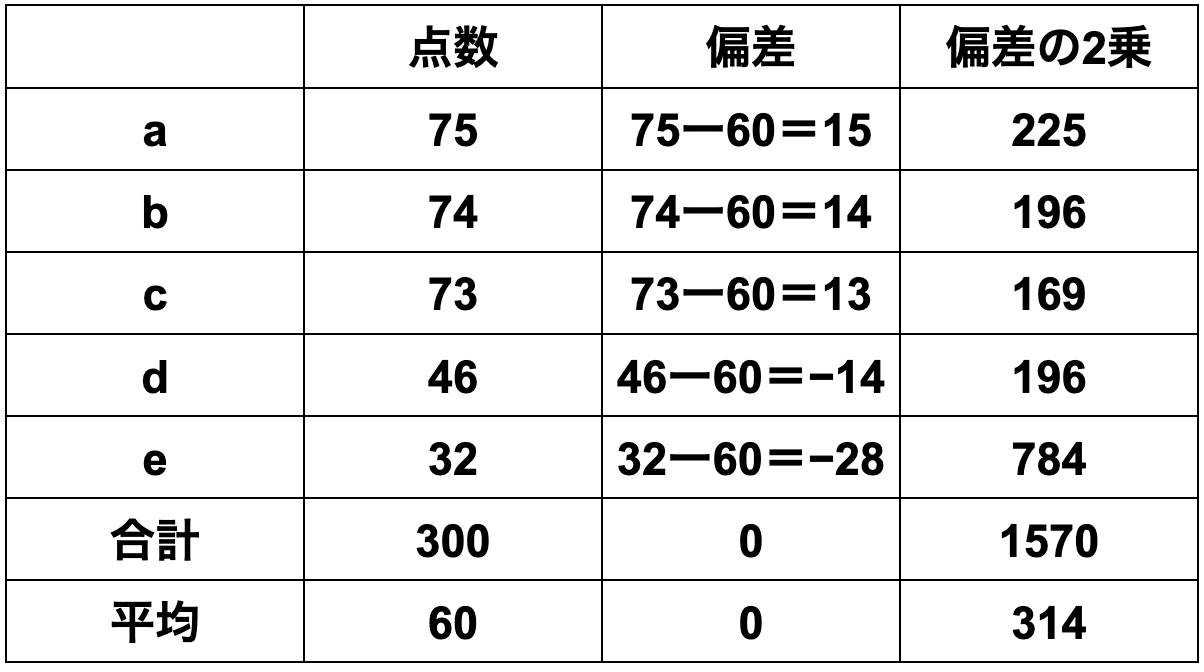
2組は、

①平均値＝各データの合計÷データ数

　　　　=(75+74+73+46+32)÷5

　　　　=60

②偏差＝各データの値−平均値

　　　＝[15、14、13、-14、-28]

③分散＝各データの偏差の2乗の合計÷データ数

　　　＝(225+196+169+196+784)÷5

　　　＝314

④標準偏差=√314=17.72

2組の方が標準偏差が大きいので、ばらつきが大きいことが分かります。

大学受験でよく聞く「偏差値」の定義は、

偏差値＝50+(得点ー平均点)÷標準偏差×10

です。

今回のテストの場合を考えると、

1組のAさん、2組のaさんは共に、

平均点60点で得点が75点で順位もクラスの中で1位ですが、偏差値が違います。

1組のAさんの偏差値

＝50+(75−60)÷8.48×10

=67.7

2組のaさんの偏差値

＝50+(75−60)÷17.72×10

=58.5

Aさんの方が偏差値が高いです。

データのばらつき具合によって、同じ点数でも相対的な位置が変わるのです。

「ばらつき具合を調べるなら、わざわざ2乗して平方根を取るなんて面倒なことをしなくても、平均との差を見ればいいのでは？」と思うかもしれません。

その考え方は平均偏差と呼ばれます。ですが、それには欠点があります。

例えば、10人のクラスが2つあるとして、どちらもテストの平均点が50点。

1組は40点5人、60点5人

2組は0点1人、100点1人、50点8人だとします。

2組の方が直感的にばらつきが大きいのは分かると思います。

ですが、平均との差を合計すると、

1組は全員が平均との差が10点なので100点

2組は0点と100点の人の平均との差が50点なので100点

となり、平均偏差は10点で同じになってしまいます。

ばらつきの大きさを正しく測るために、平均から離れれば離れるほど数値を大きくするために2乗するのです。

2乗の場合、プラスマイナスを考えなくて済むというメリットもあります。

単位を戻すために平方根を取ります。

標準偏差が分かったところで、ボリンジャーバンドの定義について話します。

20日間の終値から算出した標準偏差をσとした時に、20日移動平均線を中心として、

標準偏差×2を足したものを+2σ線

標準偏差×2を足したものを−2σ線

といいます。

じゃあ、一体ボリンジャーバンドで何が分かるのかというと、ボラティリティが分かります。

テストの話に戻すと、

1組の標準偏差が8.48

2組の標準偏差が17.72

標準偏差がデータのばらつき具合を表すということは、

逆にいうと、平均点からプラスマイナス標準偏差のところの範囲にデータがあるだろうということが分かります。

1組なら60±8.48＝51.52〜68.48点

2組なら60±17.72=42.28〜77.72点

実際に見てみると

標準偏差±1個分の中に

1組はB、C、Dさん

2組はa、b、c、dさん

では、もう少し範囲を広げて標準偏差±2個分にするとどうなるか

1組なら60±8.48×2＝43.04〜76.96点

2組なら60±17.72×2=24.56〜95.44点

こうすると、1組も2組も全員の点数が標準偏差±2個分の中に収まっています。

この考え方から、ボリンジャーバンドの±2σの範囲に価格が収まる確率が95.5%という主張があるのです。

しかし、これが成り立つのはデータのばらつき具合が正規分布の時の話。

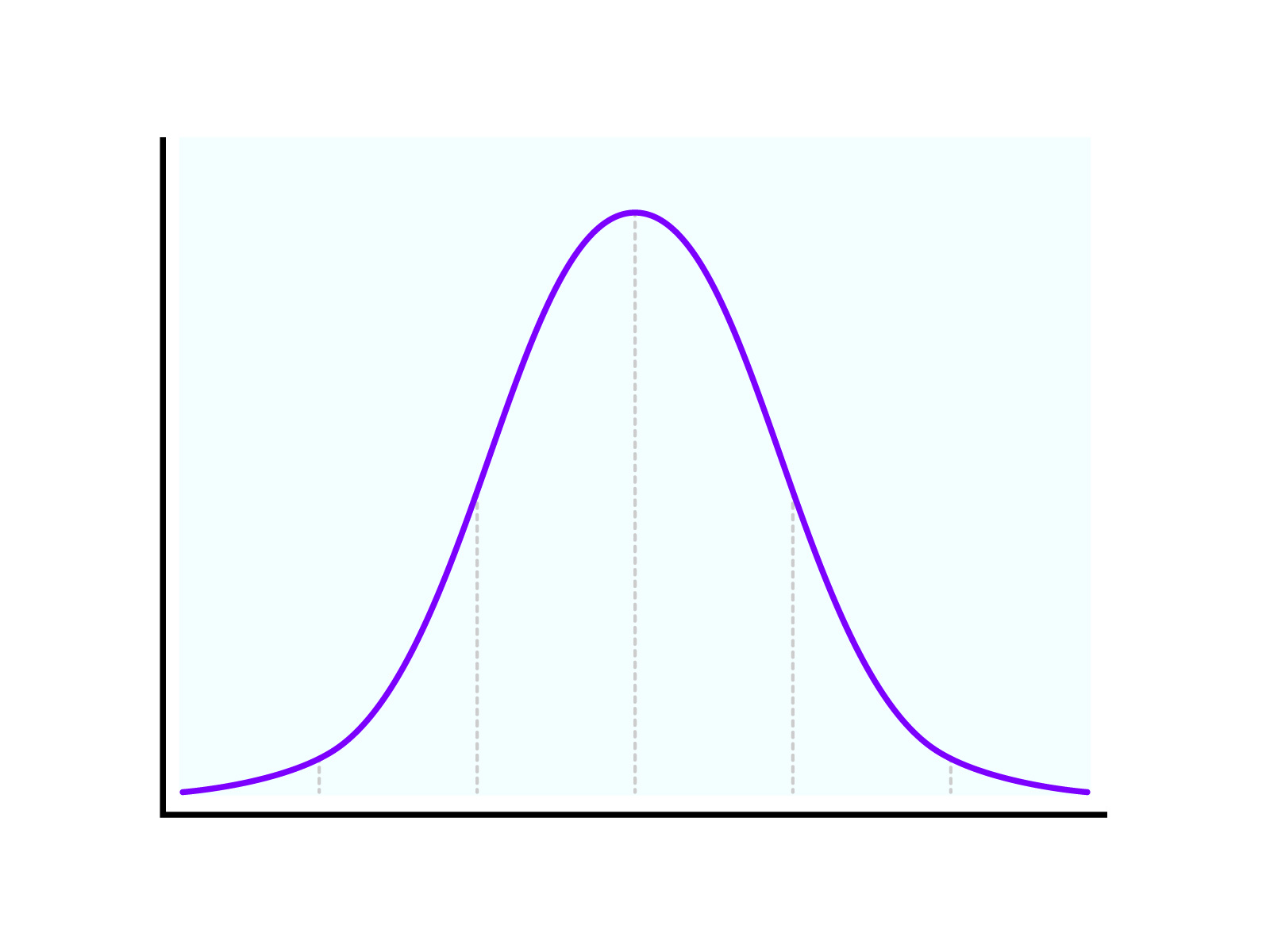
正規分布とは「平均値・中央値・最頻値が一致し、それを軸として左右対称となっている確率分布」のこと。

平均値＝データの値の合計÷データの個数

中央値＝データを小さい順に並べたとき、ちょうど真ん中にくる値

最頻値＝データの中で最も個数が多い値

人の身長の分布などがいい例です。

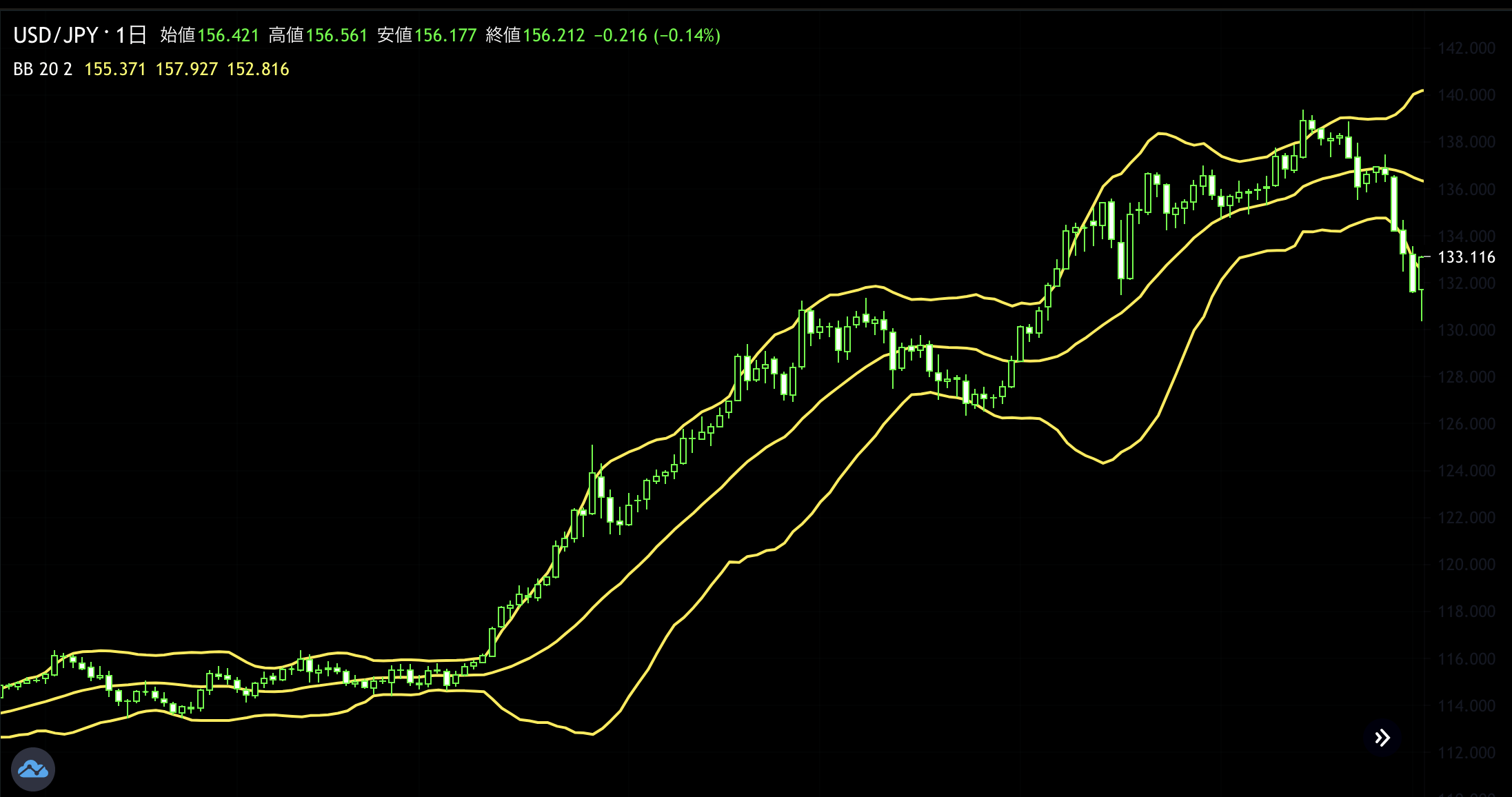
価格の動きは正規分布ではないので、問題にある主張は誤り。

価格が＋2σを超えることが頻繁にあるわけではないの事実。

しかし、＋2σに来て価格が中心に戻るのと、価格が下がるというのはイコールではない！

ネットや本に書かれている一般的なボリンジャーバンドの解説の間違いについて理解できたでしょうか。

±2σを超える確率は5%未満だから、価格が反転するだろうというのは誤り。

価格の動きは偏っているので、±2σの範囲に価格が収まるという考え方はやめましょう。

次回は、ボリンジャーバンドは3つの視点で見るという話をします。